OneLMS | Moving Load

Course / Course Details

Moving Load

nGen

By - Midas IT TH
3 students
5 Min
(0)

Course Requirements

ลงทะเบียนหลักสูตร Moveing Load

ในการบรรยายครั้งนี้ เราจะเรียนรู้เกี่ยวกับแนวคิด หลักการ และพฤติกรรมของโครงสร้างที่มีภาระเคลื่อนที่ นอกจากนี้ เราจะเรียนรู้เกี่ยวกับแนวคิดของไดอะแกรมเส้นอิทธิพลและประโยชน์ในการวิเคราะห์ภาระเคลื่อนที่

Course Description

เกี่ยวกับหลักสูตรนี้

บทที่ 1) แนวคิดการวิเคราะห์ภาระเคลื่อนที่

บทนำสู่ภาระเคลื่อนที่
วิธีการกำหนดภาระเคลื่อนที่ใน Midas Civil
หลักการของ Müller-Breslau สำหรับไดอะแกรมเส้นอิทธิพล
ภาระเคลื่อนที่และไดอะแกรมเส้นอิทธิพล

บทที่ 2) ตัวอย่าง

การสร้างแบบจำลอง การกำหนดเงื่อนไขขอบเขต การใช้ภาระเคลื่อนที่โดยใช้ Midas Civil
การวิเคราะห์และเปรียบเทียบผลลัพธ์สำหรับคานต่อเนื่องที่มีภาระเคลื่อนที่ด้วยการคำนวณด้วยมือ

บทสรุป

คุณลักษณะการวิเคราะห์ น้ำหนักบรรทุกเคลื่อนที่ ของ Midas Civil ใช้เพื่อสะท้อนให้เห็นเงื่อนไขของน้ำหนักบรรทุกสดหรือน้ำหนักบรรทุกเคลื่อนที่ของยานพาหนะแบบคงที่ และส่วนใหญ่ใช้ในลักษณะต่อไปนี้:

การหาเส้นอิทธิพลและพื้นผิวอิทธิพลสำหรับการเบี่ยงเบน แรงภายใน และปฏิกิริยาที่เกิดจากการเคลื่อนที่ของโหลด
การใช้เส้นอิทธิพลและพื้นผิวอิทธิพลที่ได้มาเพื่อคำนวณและตรวจสอบการเบี่ยงเบนสูงสุด/ต่ำสุด แรงภายใน และปฏิกิริยาจุดสำหรับสภาวะการเคลื่อนที่ของโหลดของยานพาหนะที่กำหนด

การวิเคราะห์ภาระเคลื่อนที่จะทำการวิเคราะห์ภาระที่เกิดจากภาระเคลื่อนที่หรือภาระของยานพาหนะที่เคลื่อนที่ผ่านโครงสร้าง และคำนวณค่าสูงสุดหรือต่ำสุดสำหรับเส้นทางการรับน้ำหนักทั้งหมด

เส้นอิทธิพลหรือพื้นผิวอิทธิพลมีประโยชน์ในการค้นหาตำแหน่งของแรงภายในสูงสุดโดยไม่จำเป็นต้องวิเคราะห์ซ้ำ

สำหรับภาระของยานพาหนะ จะมีการกำหนดช่องทางหรือพื้นผิวช่องทางที่จะรับน้ำหนักของยานพาหนะและวิธีการใช้ภาระของยานพาหนะ และเส้นอิทธิพลหรือพื้นผิวอิทธิพลจะคำนวณโดยโหลดภาระหน่วยบนช่องทางหรือพื้นผิวช่องทาง

เส้นอิทธิพลคือการวิเคราะห์แบบสถิตของส่วนประกอบโครงสร้างตามแนวโครงสร้างโดยโหลดหน่วยน้ำหนักและแสดงผลของแต่ละส่วนประกอบบนเส้นโครงสร้าง

พื้นผิวอิทธิพลแสดงผลของการวิเคราะห์องค์ประกอบแผงที่อยู่ภายในพื้นผิวโครงสร้างโดยการใช้หน่วยน้ำหนักกับโหนดของแผง

กระบวนการของการใช้เส้นอิทธิพลหรือพื้นผิวอิทธิพลสำหรับการวิเคราะห์น้ำหนักเคลื่อนที่สามารถสรุปได้ดังนี้:

1. กำหนดน้ำหนักเคลื่อนที่ วิธีการใช้น้ำหนัก และช่องทางหรือพื้นผิวช่องทาง

2. สร้างเงื่อนไขน้ำหนักเคลื่อนที่และดำเนินการวิเคราะห์แบบสถิตสำหรับน้ำหนักเคลื่อนที่แต่ละหน่วยเพื่อคำนวณเส้นอิทธิพลหรือพื้นผิวอิทธิพลสำหรับแต่ละส่วนประกอบ

3. ใช้เส้นอิทธิพลหรือพื้นผิวอิทธิพลตามวิธีการใช้น้ำหนักเพื่อกำหนดตำแหน่งของน้ำหนักเคลื่อนที่ และคำนวณผลการวิเคราะห์ตามนั้น

ผลการวิเคราะห์ที่ได้จากกระบวนการเหล่านี้มีการตีความสองแบบ คือ สูงสุดและต่ำสุด สำหรับเงื่อนไขการรับน้ำหนักเคลื่อนที่หนึ่งเงื่อนไข และสามารถนำไปรวมกับเงื่อนไขการรับน้ำหนักอื่นๆ ได้

เนื่องจากเงื่อนไขการรับน้ำหนักเคลื่อนที่มีการตีความสองแบบ คือ สูงสุดและต่ำสุด ผลลัพธ์ที่รวมกันจึงมีการตีความสองแบบ คือ สูงสุดและต่ำสุดด้วย

ผลการวิเคราะห์ประกอบด้วยการเคลื่อนตัวของข้อต่อ แรงปฏิกิริยาจุด โครงถัก คาน และแรงภายในขององค์ประกอบแผ่น

โหลดต่อหน่วยของเส้นอิทธิพลหรือพื้นผิวอิทธิพลที่ใช้ในการวิเคราะห์การรับน้ำหนักเคลื่อนที่จะทำหน้าที่ในทิศทาง -Z ของระบบพิกัดทั่วโลก และไม่มีข้อจำกัดในจำนวนเงื่อนไขการวิเคราะห์การรับน้ำหนักเคลื่อนที่ที่สามารถใช้ได้

ตามหลักการของมุลเลอร์-เบรสเลา เส้นอิทธิพลแสดงถึงรูปร่างของการเสียรูปของโครงสร้างเมื่อมีการนำการเคลื่อนตัวของหน่วยเข้ามาที่ตำแหน่งที่ปฏิกิริยาหรือแรงตัดขวางจะเกิดขึ้น ปฏิกิริยาหรือแรงตัดขวางในโครงสร้างสามารถหาได้จากรูปร่างของเส้นอิทธิพล

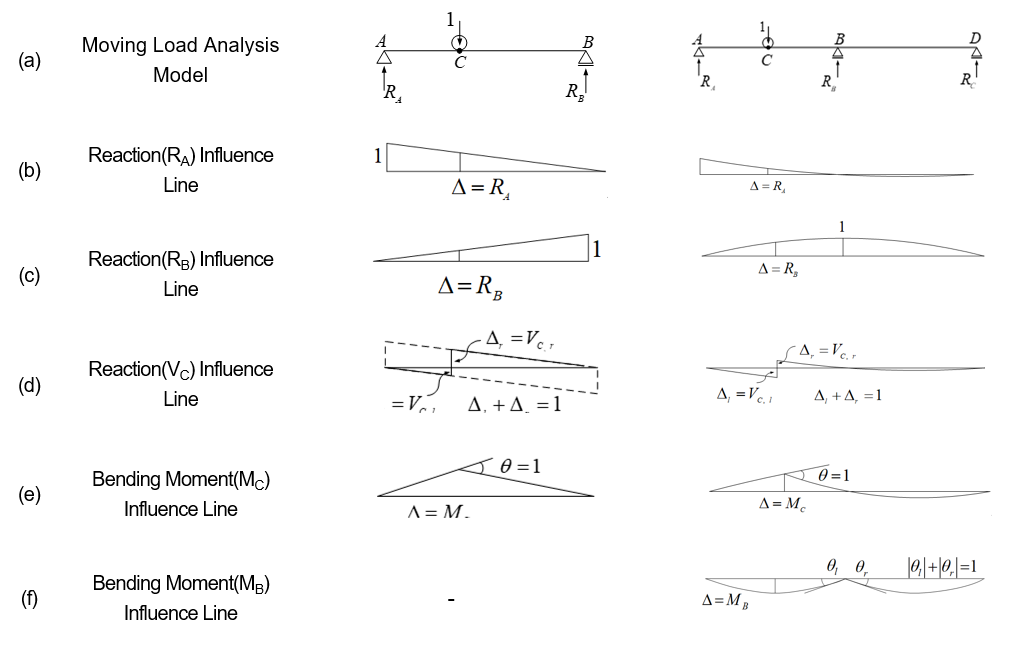
รูปที่ 10.1 แสดงเส้นอิทธิพลสำหรับคานธรรมดา และรูปที่ 10.2 แสดงเส้นอิทธิพลสำหรับคานต่อเนื่องสองช่วง

รูปที่ 10.1 แสดงเส้นอิทธิพลของปฏิกิริยาที่จุด A และ B และแรงเฉือนและโมเมนต์ที่ตำแหน่งใดก็ได้สำหรับคานธรรมดา

รูปที่ 10.2 แสดงเส้นอิทธิพลของปฏิกิริยาที่จุด A, B และ D ตลอดจนแรงเฉือนและโมเมนต์ที่จุด B และ C สำหรับคานต่อเนื่องสองช่วง

จะเห็นได้ว่าเส้นอิทธิพลของโครงสร้างที่กำหนดแบบสถิต เช่น คานธรรมดา ประกอบด้วยเส้นตรง ในขณะที่เส้นอิทธิพลของโครงสร้างที่กำหนดแบบสถิต เช่น คานต่อเนื่องสองช่วง ประกอบด้วยเส้นโค้ง

ค่าที่ทำเครื่องหมายด้วย ∆ ณ จุดที่โหลดกระทำบนเส้นอิทธิพลนั้นแสดงถึงค่าของปฏิกิริยาหรือแรงของส่วนที่เกี่ยวข้องเมื่อโหลดถูกนำไปใช้ที่จุดนั้น

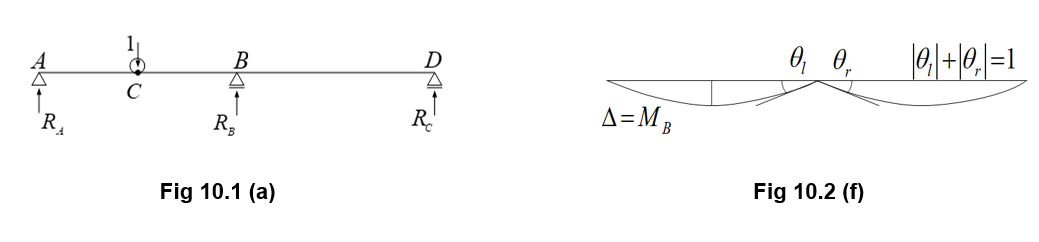
ในการอธิบายวิธีการคำนวณแรงหน้าตัดโดยใช้เส้นอิทธิพล เรามาคำนวณโมเมนต์กลางช่วง 𝑀 สำหรับคานต่อเนื่องสองช่วงตามที่แสดงในรูปที่ 10.2(f)

เนื่องจากเรากำลังจัดการกับเส้นอิทธิพลสำหรับโมเมนต์ เราจึงสอดบานพับที่จุด B เพื่อปลดโมเมนต์และใช้การหมุนหนึ่งหน่วยที่จุดนั้นเพื่อสร้างรูปร่างการเสียรูปที่แสดงถึงเส้นอิทธิพล

ค่า ∆ ที่จุดกึ่งกลางของช่วง AB แทนค่า 𝑀_𝐵 เมื่อโหลดเคลื่อนที่อยู่ที่จุดนั้น เนื่องจากโครงสร้างสมมาตรเทียบกับจุด B เราจึงได้ ∆= 𝑀_𝐵 สำหรับด้านหนึ่งของคานธรรมดาเมื่อใช้โมเมนต์ 𝑀